Table of Contents
ToggleWhen it comes to math, fractions can feel like the unruly cousins at a family reunion—hard to manage but oddly fascinating. Take the expression (1/2)^2, for example. It’s a tiny fraction with a big impact, and understanding it can unlock a world of mathematical wonders. Whether you’re a math whiz or someone who still counts on their fingers, this little number packs a punch that’s worth exploring.
So why should anyone care about squaring a half? Well, beyond the math, it’s a gateway into the realms of ratios, percentages, and even real-world applications like cooking and budgeting. Plus, who doesn’t love a good math joke? Spoiler alert: it’s all about getting to the “whole” truth! Join the journey to discover how this seemingly simple calculation can lead to some surprisingly profound insights.
Understanding Fractions
Fractions represent parts of a whole. This essential concept underpins many mathematical principles and real-world applications.
What Are Fractions?
Fractions consist of two parts: the numerator and the denominator. The numerator indicates how many parts are being considered, while the denominator shows the total number of equal parts. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2. Each fraction can also be expressed as a decimal or percentage, expanding its utility across various contexts.
Importance of Fractions in Mathematics
Fractions play a crucial role in mathematics. They assist in operations such as addition, subtraction, multiplication, and division. Understanding fractions enables clearer communication in fields like science, engineering, and finance. For instance, ratios, rates, and proportions often utilize fractions. Application extends to everyday tasks too, such as measuring ingredients in cooking or sharing resources in budgeting. Recognizing the significance of fractions enhances mathematical comprehension and practical problem-solving skills.
Exploring (1/2)^2
The value of (1/2)^2 serves as a fundamental concept in mathematics. Understanding its definition enhances comprehension of fractions and their applications.
Definition and Calculation
(1/2)^2 signifies squaring the fraction one-half. To calculate this, multiply the numerator by itself and the denominator by itself. Therefore, 1 × 1 equals 1, and 2 × 2 equals 4. Thus, the result of (1/2)^2 is 1/4. This fractional outcome shows how squaring a fraction results in a smaller value. Moreover, recognizing this relationship becomes essential, particularly in scenarios involving scaling down quantities or calculating areas.
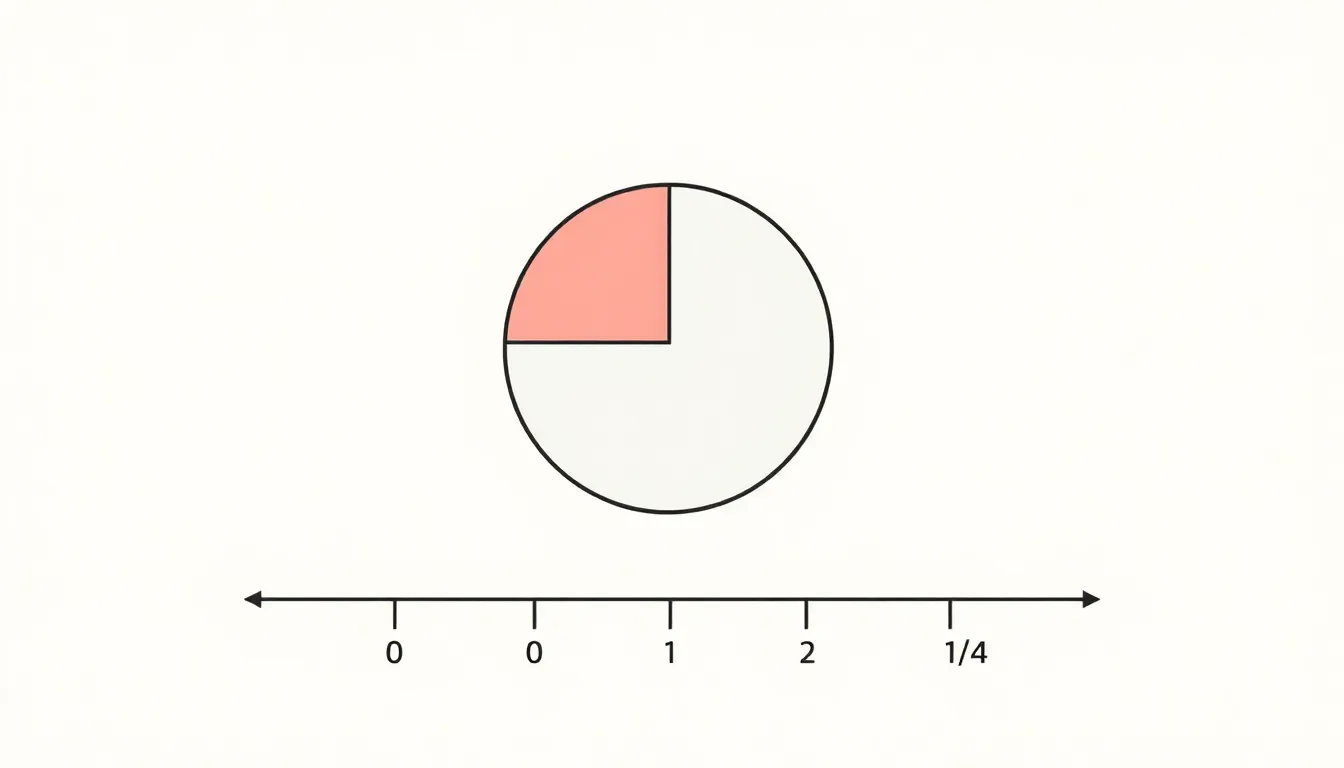
Visual Representation
Visualizing (1/2)^2 aids in grasping its meaning. A pie graph effectively illustrates one-half as one of two equal parts. When squaring this fraction, the pie can be divided into four equal sections. The shaded area representing 1/4 showcases how one-half squared translates into one quarter. Additionally, using number lines creates further clarity. Marking 0, 1/2, and 1/4 on the line highlights the fraction’s position relative to whole numbers. This visual representation reinforces understanding of fractions and their squared equivalents.
Applications of (1/2)^2
Understanding (1/2)^2 showcases its practical uses in various fields, illustrating its impact on everyday calculations.
Real-World Examples
In cooking, adjusting recipes often requires squaring fractions. For instance, halving a recipe and then needing to halve it again involves calculating (1/2)^2, which equals 1/4. This specific example exemplifies how culinary professionals adapt ingredient quantities. Budgeting also requires similar calculations. Individuals might need to divide expenses, leading to scenarios where determining one-fourth of a total cost is essential. Another practical use emerges in home improvement projects, where measurements often need scaling. Accurately calculating areas, such as flooring in a room that is half the size of another, involves squaring fractions to find the required dimensions.
Importance in Geometry
Squaring fractions plays a key role in geometry, especially when calculating areas of geometric shapes. For example, the area of a square relies on the square of its side length. If a square has a side length of (1/2), squaring it produces an area of 1/4. This example highlights how fractions appear in various geometric applications, simplifying area calculations. Architects and engineers frequently apply these principles. Understanding the implications of (1/2)^2 assists in designing structures that maintain proportion and stability. Moreover, it supports optimization in geometric problems, ensuring accurate and efficient solutions in fields that require precision.
Common Misconceptions
Many people confuse fractions with whole numbers, thinking squaring a fraction simply results in the same whole number squared. For example, when they see (1/2)^2, they might mistakenly believe the answer mirrors that of 1^2, resulting in 1. This misunderstanding often leads to inaccuracies in calculations.
Another common misconception involves miscalculating the squared value itself. Some assume that fractions do not change in value when squared. Yet, (1/2)^2 equals 1/4, which highlights that squaring a fraction reduces its value, leading to smaller results than expected.
Misinterpretations frequently occur with concepts of area too. Many individuals may overlook that squaring relates directly to area, particularly when discussing geometric shapes. For instance, calculating the area of a square with a side length of (1/2) using (1/2)^2 yields an area of 1/4, not a larger measurement.
Additionally, some may neglect recognizing the importance of context when applying fractions. In practical situations like cooking or budgeting, failing to understand (1/2)^2 can result in significant errors, impacting recipe adjustments or total cost estimations.
Lastly, learners often struggle with the transition from fractions to decimals. Misconceptions arise when they can’t connect the fraction form to its decimal equivalent. Understanding that 1/4, derived from (1/2)^2, translates to 0.25 can clarify relationships between different numerical representations. Addressing these misconceptions fosters a more comprehensive grasp of fractions and their applications in real-life scenarios.
Understanding the squaring of fractions like (1/2)^2 deepens one’s grasp of mathematical concepts and their real-world applications. This knowledge not only aids in everyday tasks such as cooking and budgeting but also enhances problem-solving skills in various fields. Recognizing the nuances of fractions and their squared values can prevent common misconceptions and inaccuracies. As individuals become more comfortable with these concepts, they unlock new levels of mathematical comprehension that can be beneficial in both academic and practical situations. Embracing the complexity of fractions enriches one’s understanding of mathematics and its relevance in everyday life.




